Class 10 Maths Exercise 10.2 Solutions
Class 10 Maths Exercise 10.2 in Hindi
Class 10th Maths NCERT Book Download
10th Maths Chapter 10 Solutions
Class 10 Maths NCERT Solutions
Class 10 all Subjects NCERT Solutions
NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2 Circles in Hindi and English Medium updated for board exams 2024-25 CBSE and State board students. The explanation of each question of 10th Maths exercise 10.2 is simplified in such a way that every student can understand comfortably.
Class 10 Maths Exercise 10.2 Questions in Detail
- From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is (A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5 cm
- If TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to (A) 60° (B) 70° (C) 80° (D) 90°
- If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to (A) 50° (B) 60° (C) 70° (D) 80°
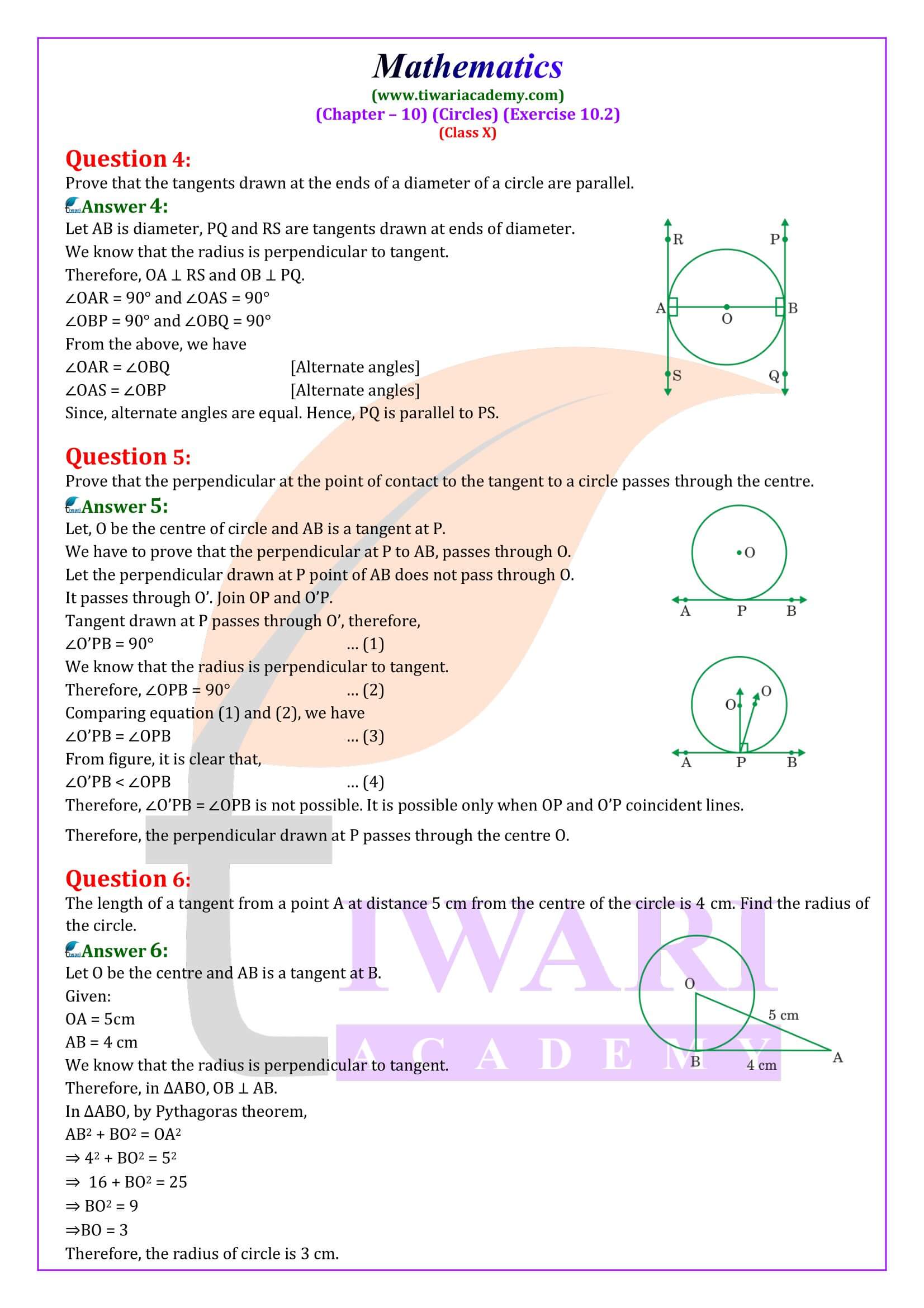
- Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
- Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
- The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
- Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
- A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.
- If XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
- Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
- Prove that the parallelogram circumscribing a circle is a rhombus.
- A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
- Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
| Class: 10 | Maths Solutions |
| Chapter: 10 | Circles |
| Contents: | Exercise 10.2 |
| Updates: | CBSE Session 2024-25 |
| Medium: | English and Hindi Medium |

NCERT Solutions Class 10 Maths Chapter 10 Exercise 10.2
Class 10 Maths Ex. 10.2 download in PDF format free in Hindi Medium and English Medium updated for new academic session 2024-25 based on latest NCERT Books 2024-25. NCERT Solutions and Offline Apps are free to use or View in Video Format for all the students (CBSE, UP Board and other board) using NCERT Books as a course book. NCERT Solutions and Offline Apps are updated for the new academic session 2024-25.
10 Maths Chapter 10 Exercise 10.2 Solutions
NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2 Circles in Hindi as well as English Medium free to use for CBSE, UP Board, MP Board and all other boards who are using NCERT Textbooks 2024-25. Visit to Class 10 Maths Chapter 10 main page for other exercises whether download or online study.
Class 10 Maths Exercise 10.2 Solution in Hindi Medium
Class 10 Maths Chatper 10 Exercise 10.2 Solutions in Videos
About 10 Maths Exercise 10.2
Most of the questions in Exercise 10.2 are based on Tangent ⊥ Radius and then solve it by Pythagoras Theorem. Question no. 8 and 9 are based on “Tangents drawn from same external points are equal”. Question no. 11 is same as question 8, only one or two more steps are required. Question no. 13 is based on question no. 9. Question no. 12 is the most important question as it is asked in CBSE board exams several times.
Questions for Practice on Circles
1. The length of the tangent to a circle from a point P, which is 25 cm away from the centre, is 24 cm. What is the radius of the circle.
2. If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then find the length of each tangent.
3. If radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
4. The length of tangent to a circle of radius 2.5 cm from an external point P is 6 cm. Find the distance of P from the nearest point of the circle.
5. TP and TQ are the tangents from the external point T of a circle with centre O. If angle OPQ = 30° then find the measure of angle TQP.
Ask your doubts related to NIOS or CBSE Board and share your knowledge with your friends and other users through Discussion Forum and download CBSE NCERT Books for offline use.
How many examples and questions are there in exercise 10.2 of class 10th Maths?
There are 3 examples (Examples 1, 2 and 3) and 13 questions in exercise 10.2 of class 10th math. All examples and questions are of different type. Also all examples and questions are important from exam point of view. Any question and example of this exercise can come in exam.
Is exercise 10.2 of class 10 Maths easy?
No, exercise 10.2 of class 10 math is not an easy exercise. Some questions of this exercise are easy and some are difficult. But difficulty level of anything varies from student to student. So, Exercise 10.2 (chapter 10) of class 10th mathematics is easy or not depends on students also.
What are the questions from exercise 10.2 of class 10 Maths that students find interesting?
Question 1, 2, 3, 4, 6 and 8 of exercise 10.2 (class 10 math) are student’s favourite questions because these questions are easy to understand as compare to other questions of this exercise and students solve these questions without any difficulty. Also solutions of these questions are short in length.
What is the minimum duration to complete exercise 10.2 (chapter 10) of class 10th mathematics?
Students need maximum 5-6 days to complete exercise 10.2 (chapter 10) of class 10th mathematics. This time depends on student’s speed and capability also.